Soft Light

Soft Light is the one blend mode I read most nonsense about. Part of this may be due to the fact that vendors define the method differently, get quoted incorrectly and thus add to the confusion. Alas, I couldn’t find explanations for their particular choices, so I can only show what I figured out and present my own thoughts.

Photoshop

My Photoshop CC uses the following formula (as documented in PDF Reference):

$f(a,b) = \left\{ \begin{array}{lr}(1-a)ab + a(1-(1-a)(1-b)) & \text{for } b < {1/2}\\a+(2b-1)(\sqrt{a}-a) & \text{f\"ur } b \geq {1/2} \land a > {1/4}\\a+(2b-1)(((16a-12)a+4)a-a) & \text{for } b \geq {1/2} \land a \leq {1/4}\end{array} \right.$

I was able to verify that with the help of a little Postscript script may father generously provided (thank you very much for your support, (Dieter)). It fills a square with the result of a blend between two linear gradients using a formula only limited by your Postscript skills (reverse Polish notation). After comparing the result with Photoshop’s own blend, I can assure you now that this indeed is the formula used, whatever others try to tell you. (For more details about the process see here).

The two source images:

Gradient A — Image A – horizontal gradient

After blending using the Soft Light formula with the Postscript script:

Soft Light calculated — Calculated Soft Light

and using Photoshop’s Soft Light blend mode:

By subtraction one can easily show both images are identical (but for small deviations due to limited resolution and rounding errors).

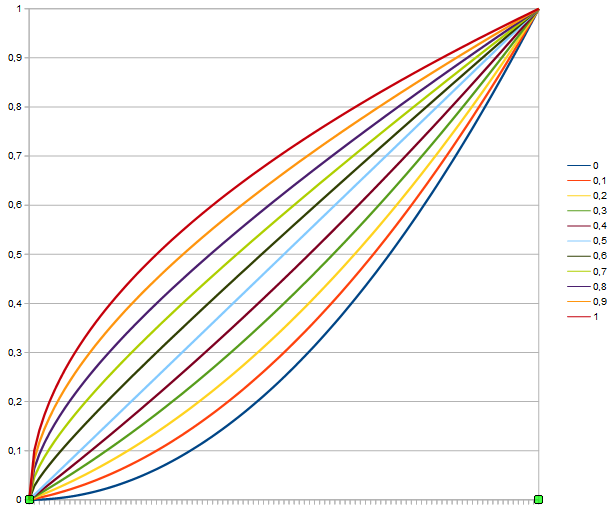
A closer look at the brightness for fixed b-values is quite interesting:

As you can see for b=0,5 you get the diagonal, i.e. a linear translation from a to brightness. Hence if you chose an evenly grey image for B (50% grey), the image A is unchanged by the blending. Actually, this is a design goal for all formulas we are looking at here, 50% grey is supposed to be neutral.

For b=0 you get the much simpler formula:

$f(a,b) = a(1-(1-a)) = {a}^{2}$ .

This is nothing else but the γ-correction (Gamma-correction) with γ=2. The curve for b=1 looks a lot like the square root function, that would be a γ-correction with γ=0.5, but due to the corrective term for small a it is not identical.

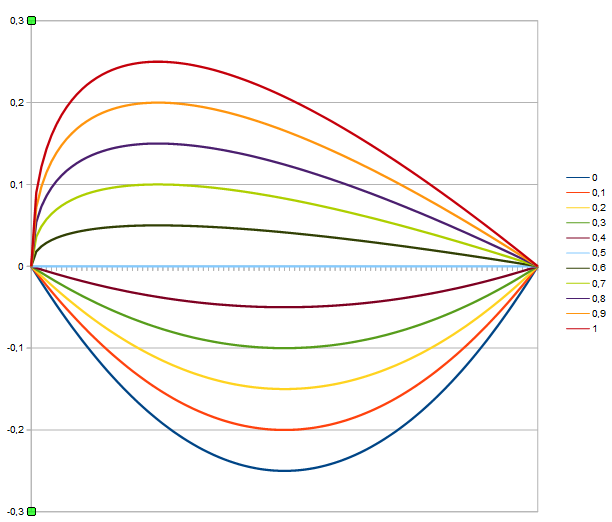
I was interested in the course of the deviation from the diagonal

$f(a,b) = a$

for different values of b, as that might show me the degree of symmetry of the method. So I plotted curves for

$f(a,b) = \left\{ \begin{array}{lr}(1-a)ab - a(1-a)(1-b) & \text{for } b < {1/2}\\(2b-1)(\sqrt{a}-a) & \text{for } b \geq {1/2} \land a > {1/4}\\(2b-1)(((16a-12)a+4)a-a) & \text{for } b \geq {1/2} \land a \leq {1/4}\end{array} \right.$

The strong asymmetry for b > 0,5 is striking.

Variations of the Soft Light formula

Using the following formula, also sometimes presented as the Photoshop-formula, you get a slightly different result. Here you actually get the γ=0.5 correction for b=1.

$f(a,b) = \left\{ \begin{array}{lr}(1-a)ab + a(1-(1-a)(1-b)) & \text{for } b < {1/2}\\a+(2b-1)(\sqrt{a}-a) & \text{for } b \geq {1/2}\end{array} \right.$

Without the corrective termfor small a — Without the “correction” for small a

At a close look you might see that the top left corner is slightly brighter than the one from Photoshop.

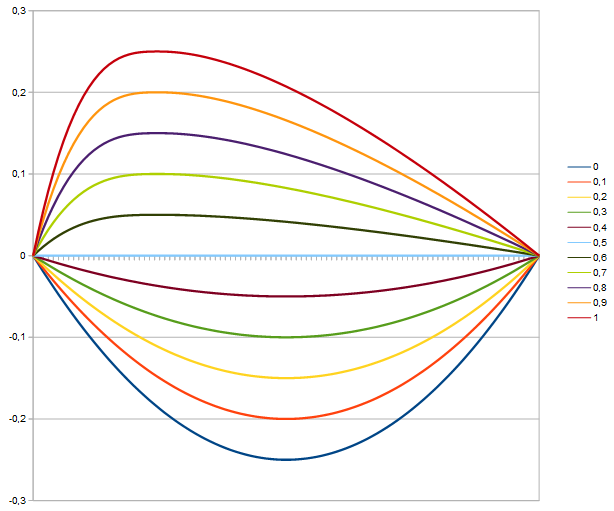
The corresponding curves look like this:

Again no symmetry. Yes, you could mirror at the diagonal, but that is not keeping a fixed. For blending we want to know how a fixed value of a would be translated for varying b. Here identical changes in b result in more or less strong effect depending on the direction you move from b=0.5. You can see this more easily after subtaction of a.

In this representation you can clearly see how strong the change of the image would be for small a. Maybe too strong for Adobe so they chose to add that corrective term?

But then, you could only use the first part of the original formula, this one:

$f(a,b) = (1-a)ab + a(1-(1-a)(1-b))$

Also a lovely, very smooth result, linear in b. This linearity you can see in the curves as well:

Now you can no longer get mirror-symmetry along the diagonal, but the distance between curves for fixed a is always the same.

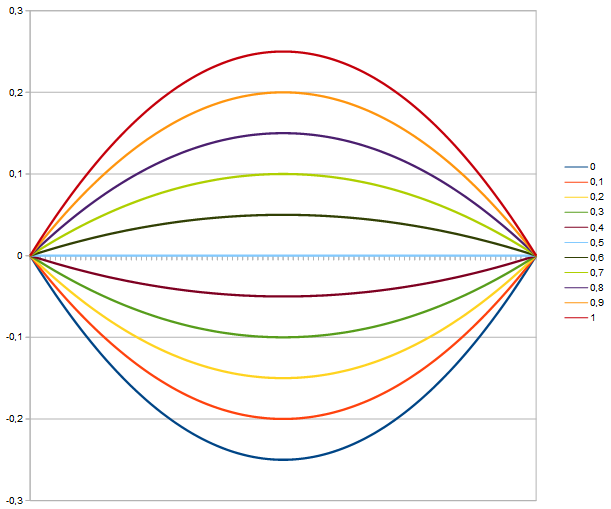Here you see symmetry, looks very plausible, but for b=1 you miss γ=0,5 by a long shot.

Illusions’ parametric Gamma-Correction

A completely different approach to Soft Light you can find at illusions.hu. Starting from the idea of a parametric γ-correction, controlled by b, they use:

$f(a,b) = a^{2^{(1-2b)}}$

The result of the blend is very pleasing, at least to my eyes:

At first glance, the curves almost look like the ones for the original Adobe-formula:

At a closer look the transitions are much smoother of course. This is not glued together from different parts, no wonder.

Mirror Games

I also have my own suggestion, a spin-off from my trying to answer the question if the second part of the Photoshop-formula might be the first mirrored at the diagonal. The answer is: it isn’t. You get the formula for the mirrored curve by resolving the first part for a and replacing by with (1-b’). The latter because for b > 0,5 the curve must be the mirror of one with b’=1-b.

$f(a,b) = \left\{ \begin{array}{lr}(1-a)ab + a(1-(1-a)(1-b)) & \text{for } b < {1/2}\\ \frac{1-b}{1-2b}+\sqrt{\frac{(1-b)^2}{(2b-1)^2}+\frac{a}{2b-1}}& \text{for } b \geq {1/2}\end{array} \right.$

In this case the deviations from the diagonal are:

I find this is not bad at all. Slightly brighter bottom left than the Illusions version, less drastic top left that the reduced Photoshop-formula (the one without the corrective for small a).

I have to admit, the whole is pretty academic. Alas, we cannot add new blend modes to Photoshop that easily. If you can, let me know. I’d love to have the last two blend modes there.

Other parts of this mini-series

Blend Modes – Part 1: Multiply, Linear Burn, Linear Dodge and Linear Light

Blend Modes – Part 2: Color Burn, Color Dodge, Screen, Overlay, Hard Light and Vivid Light

Photoshop Blend Modes - Part 3